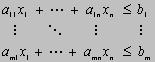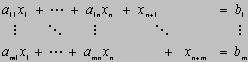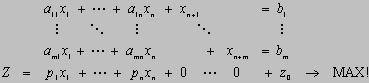Lineare Optimierung mit dem Simplexalgorithmus |
||
Inhaltsübersicht |
||
|
||
1. Einleitende Worte |
||
| In einem Leistungskurs der Jahrgangsstufe 12 habe ich
meine zweite Staatsexamensarbeit mit dem Thema "Ein Zugang zur linearen
Optimierung unter besonderer Berücksichtigung des
Simplexverfahrens" durchgeführt. Hierbei
handelte es sich um eine zwölfstündige
Unterrichtsreihe, durchgeführt im Rahmen der linearen
Algebra, und zwar im Anschluß an den Gaußalgorithmus
und die Lagebeziehungen zwischen Geraden und Ebenen. In dieser Reihe sollten sich die Schülerinnen und Schüler mit der Anwendung der linearen Optimierung vertraut machen. In diesem Zusammenhang sollten sie sowohl das graphische Lösungsverfahren als auch besonders den Simplexalgorithmus erfassen und anwenden und den Computer als Hilfsmittel zur Lösung komplexer Zusammenhänge kennenlernen. Als Software wurde das Computeralgebrasystem DERIVE eingesetzt, mit einem von mir geschriebenen Programm zur Lösung der Aufgaben mit Hilfe des Simplexalgorithmus. Im folgenden möchte ich die lineare Optimierung und insbesondere den Simplexalgorithmus vorstellen, der eine schöne Methode darstellt, lineare Optimierungsaufgaben zu lösen und dabei wunderbar auf bekanntes Wissen der Schüler aufbaut: dem Gaußalgorithmus. Dabei verwende ich u.a. Ausschnitte aus meiner Staatsexamensarbeit. Dazu gehört insbesondere der fachwissenschaftliche Hintergrund zur linearen Optimierung und dem Simplexverfahren im dritten Kapitel. Einige Überlegungen zur Planung der von mir durchgeführten Reihe werden im vierten Kapitel angerissen, ebenso wie einige reflektierende Bemerkungen. Im Anhang steht das verwendete Computerprogramm zum Downloaden zur Verfügung. Außerdem stelle ich zwei selbsterdachte Aufgaben zur linearen Optimierung vor. Eine umfaßt eine mehrstündige Gruppenarbeit. |
||
| zurück zum Inhaltsverzeichnis | ||
2. Zur Wahl des Themas |
||
| Die Idee des Optimierens spielt im Alltag eine
wichtige Rolle: am Schnellsten schwimmen, am
Preiswertesten einkaufen, den größten Gewinn machen,
die kürzeste Arbeitszeit haben usw. Viele Bereiche des
Lebes sind bestimmt vom Wunsch oder der Notwendigkeit zu
optimieren. Somit beschäftigt sich auch die Mathematik und damit auch der Mathematikunterricht mit diesem Thema. Tietze spricht sogar von einer "herausragenden Rolle" [10] für den Mathematikunterricht der Sekundarstufe II, wobei sowohl die Extremwertaufgaben aus der Analysis als auch die lineare Optimierung als Beispiele genannt werden (vgl. [10], S.40). |
||
| Der graphische Zugang zur linearen Optimierung findet
sich bereits in den Schulbüchern der Klassen 8 und 9 als
Ergänzungsstoff zur Beschäftigung mit linearen
Ungleichungssystemen mit zwei Variablen. Die Menge des
regulären Unterrichtsstoffes läßt in der Regel aber
keine Zeit, sich mit diesem Thema auseinanderzusetzen. Der Bereich der linearen Algebra bietet inhaltlich eine zweite Möglichkeit, sich mit diesem wichtigen Thema zu befassen, ebenfalls als natürliche Erweiterung der linearen Gleichungssysteme auf lineare Ungleichungssysteme, hier allerdings auch mit mehr als zwei Unbekannten. Wurden vorher beispielsweise überhaupt mögliche Sandmischungen gesucht, so fragt man nun nach der optimalen Sandmischung, z.B. unter dem Gesichtpunkt eines bestmöglichen Gewinns. |
||
| Analog zur Beziehung zwischen den linearen Ungleichungen und den linearen Gleichungen gibt es eine Beziehung zwischen den Lösungsverfahren: Der zur Lösung der Optimierungsaufgabe herangezogene Simplexalgorithmus läßt sich auf den zur Lösung der linearen Gleichungssysteme verwendeten Gaußalgorithmus zurückführen. So können die Schüler hier auf ein ihnen bekanntes Verfahren aufbauen. | ||
| zurück zum Inhaltsverzeichnis | ||
3. Der fachwissenschaftliche Hintergrund |
||
| Die von mir gewählte Darstellung der linearen
Optimierung und des Simplexalgorithmus wurden so
gewählt, daß sie den Einsatz des Gaußalgorithmus
ermöglichen, den die Schüler im Rahmen der linearen
Algebra erarbeiten. Die Idee baut auf die Behandlung der
linearen Optimierung im Buch Mathematik zur
Fachhochschulreife von Schöwe, Knapp und Borgmann,
Cornelsen Verlag, Berlin, 1996 [1] auf. Bem.: In der fachwissenschaftlichen Literatur stehen andere Aspekte im Vordergrund, z.B. eine durchgängige Theorie (vgl. [3], S.203ff), eine performante Programmierung (vgl. [5], S.430ff) oder auch eine komprimierte Darstellung [vgl. [6], S.695ff). Dabei wird die Notation dem jeweiligen Schwerpunkt angepaßt und ist daher uneinheitlich. |
||
3.1 Die Begrifflichkeit der linearen Optimierung |
||
|
||
| Eine lineare
Optimierungsaufgabe besteht aus: 1. Zielfunktion: 2. Nebenbedingungen: 3. Nicht-Negativitätsbedingungen: mit natürlichen Zahlen n und m und
reellen Koeffizienten |
||
Die Zielfunktion beschreibt den zu optimierenden Wert
in Abhängigkeit von den Problemvariablen
 .
Die Nebenbedingungen und die Nicht-Negativitätsbedingung
beschreiben den Bereich für die erlaubten Werte dieser
Variablen, den sogenannten Lösungsbereich,
der aber insbesondere bei geometrischen Betrachtungen
auch als Planungsgebiet
bezeichnet wird. Die Zielfunktion wird ausschließlich
für Werte aus dem Lösungsbereich betrachtet. Die
Aufgabe besteht darin, für die Variablen
reelle Werte mit folgenden Eigenschaften zu finden:
|
||
| Man nennt Werte, für die diese beiden Eigenschaften erfüllt sind, eine optimale Lösung der Optimierungsaufgabe. Variablen-Werte, die die zweite Bedingung erfüllen, nennt man zulässige Lösung. | ||
| Auf die Unterscheidung zwischen Maximums- und Minimumsaufgaben kann man bei theoretischen Überlegungen verzichten, da durch den Übergang von Z zu -Z jede Minimumsaufgabe zu einer Maximumsaufgabe wird und umgekehrt. Beim Simplexalgorithmus treten bei Minimumsaufgaben jedoch zusätzliche Aspekte auf, die in der Reihe nicht behandelt werden. | ||
Um die Struktur und das Vorgehen bei linearen
Optimierungsaufgaben kennenzulernen, genügt die
Betrachtung von regulären
linearen Optimierungsaufgaben. Dies sind lineare
Optimierungsaufgaben mit zwei Einschränkungen:
In der Unterrichtsreihe wurden ausschließlich solche regulären linearen Optimierungsaufgaben untersucht. |
||
3.2 Der mathematische Kontext |
||
| Es gibt im wesentlichen zwei Schnittstellen zwischen der linearen Optimierung und anderen mathematischen Bereichen. Die lineare Optimierung ist einerseits eine Erweiterung der Betrachtung von linearen Gleichungen, andererseits ein Spezialfall der allgemeinen mathematischen Optimierung. | ||
3.2.1 Die Beziehung zu linearen Gleichungen |
||
| Die Nebenbedingungen werden durch lineare
Ungleichungen beschrieben. Wenn man zu jeder dieser
Ungleichungen eine reelle, nicht-negative zusätzliche
Variable (Schlupfvariable
genannt) hinzufügt, so kann man die Ungleichungen in
Gleichungen überführen: |
||
| Deshalb kann man für die lineare Optimierung Methoden aus dem Bereich der Lösung linearer Gleichungssysteme einsetzen. Insbesondere für den Simplexalgorithmus spielt das Gaußverfahren bzw. die Pivotierung eine große Rolle. | ||
3.2.2 Die Beziehung zur allgemeinen Optimierung |
||
Ein allgemeines mathematisch formuliertes
Optimierungsproblem, bestehend aus einer Funktion, der
Einschränkung ihres Definitionsbereiches und der
Aufgabe, ein Extremum zu finden, löst man in zwei
Schritten:
Anschließend sind nur noch die gefundenen Werte zu vergleichen und das Minimum bzw. das Maximum zu bestimmen. |
||
| Für die Bearbeitung des ersten Schrittes kann man
seit Newton und Leibniz die Differentialrechnung
benutzen. Dadurch transformiert man die
Optimierungsaufgabe in ein Nullstellenproblem. Das Ermitteln der Extrema auf dem Rand des Definitionsbereichs ist bei einem eindimensionalen Definitionsbereich leicht, da jedes kompakte Intervall auf dem Zahlenstrahl genau zwei Randpunkt hat. In höheren Dimensionen verwendet man das Verfahren der Lagrangen Multiplikatoren und gelangt dann zu einem Gleichungssystem, welches häufig nur sehr aufwendig gelöst werden kann. Glücklicherweise sind viele in der Wirklichkeit vorkommende Optimierungsaufgaben linear, wie z.B. die Maximierung von Gewinnen in der Landwirtschaft, die Maximierung von Erträgen in Supermärkten, die Minimierung von Abgasen bei LKW-Transporten, und viele mehr. |
||
3.3 Die graphische Lösung |
||
| Bei zwei Variablen (n = 2) kann man lineare
Optimierungsaufgaben graphisch lösen. Die
Nicht-Negativitätsbedingungen beschreiben den ersten
Quadraten in der zweidimensionalen euklidischen Ebene,
jede der Nebenbedingungen beschreibt eine durch eine
Gerade gegrenzte Halbebene, die Zielfunktion beschreibt
für jedden festen Funktionswert Z eine Gerade.
Die Menge dieser Geraden bildet eine parallele
Geradenschar mit einer festen Steigung. Man zeichnet zu jeder Nebenbedingung die zugehörige Grenzgerade in die Ebene ein. Die zulässigen Lösungen liegen in der Schnittmenge der entsprechenden Halbebenen im ersten Quadranten. Dann zeichnet man eine beliebige Geradenscharmit der entsprechenden Steigung in die Ebene ein, z.B. die Gerade für Z = 0, und verschiebt diese Gerade, genannt Zielgerade, parallel. Wenn man das Maximim sucht, dann verschiebt man die Zielgerade parallel in Richtung wachsender Z- Werte, so daß aber noch mindestens ein Punkte des Planungsgebiets auf der Zielgeraden liegt. Dabei wird (im nicht-entarteten Fall) zuletzt eine Ecke erfaßt, und der Wert der Zielfunktion an dieser Ecke ist das gesuchte Optimum. Zwar kann man die Koordinaten dieser Ecke oft nicht direkt aus der Zeichnung ablesen, insbesondere wenn sie nicht ganzzahlig sind, aber man kann zumindest die grenzgeraden erkennen, die sich an der optimalen Ecke schneiden. Für diese Geraden kann dann leicht rechnerisch der Schnittpunkt bestimmt werden. |
||
| Bei mehr als zwei Variablen ist eine graphische
Lösung nicht mehr sinnvoll. Bei drei Variablen ist eine
Zeichnung oder auch ein räumliches Modell zwar möglich,
aber man kann die Lösungin der Regel nicht erkennen. Bei
mehr als drei variablen ist eine graphische Garstellung
nicht möglich. man interessiert sich in der realität aber häufig gerade für Probleme mit vielen Variablen, man denke nur an die vielen Produkte im Sortiment eines Supermarktes. Also genügt der graphische Lösungweg nicht, und man benötigt einen rechnerischen Lösungsweg, der für beliebig viele Variablen gilt. |
||
3.4 Der Hauptsatz der linearen Optimierung |
||
| Der Lösungsbereich einer linearen Optimierungsaufgabe ist ein konvexes Polyeder und wenn man keine entarteten Optimierungsprobleme (d.h. solche mit vielen optimalen Lösungen) betrachtet, gilt: | ||
|
||
Das hat Konsequenzen:
|
||
3.5 Eine naive rechnerische Lösung |
||
| Es gibt einen sehr offensichtlichen
Lösungsalgorithmus: Man berechnet die Werte der zu
optimierenden Funktion an allen Ecken des Polyeders und
nimmt dann die Ecke mit dem optimalen Zielfunktionswert. Dazu benötigt man einen Weg zur Ermittlung der Ecken des Polyeders. Diese kann man mit den Nebenbedingungen und den Nichtnegativitätsbedingungen |
||
| Die m Nebenbedingungen bilden zusammen mit
den n Nicht-Negativitätsbedingungen insgesamt n
+ m Ungleichungen. Die zu diesen Ungleichungen
gehörenden Gleichungen repräsentieren die Hyperebenen,
die das Polyeder begrenzen. Nimmt man von diesen n + m Gleichungen nun n linear unabhängige Gleichungen, so bilden diese ein lineares inhomogenes Gleichungssystem von maximalem Rang, welches eindeutig lösbar ist. Diese Lösung ist dann der Schnittpunkt der zugehörigen Hyperebenen. Es sind jedoch nur solche Schnittpunkte zugelassen, die auf dem Rand des Polyeders liegen. Um sie zu ermitteln, nimmt man von den gefundenen Schnittpunkten diejenigen, die alle Ungleichungen erfüllen. Mann könnte glauben, daß man damit das Problem gelöst hat. Aber damit geht man in die typische Falle von kombinatorischen Problemen. Man findet zwar mit dem obigen Algorithmus stets eine Lösung, aber wie lange dauert das? |
||
Bei n Variablen und m
Nebenbedingungen werden während des Laufes des
Algorithmus insgesamt bis zu  Schnittpunkte
berechnet. Bei 100 Variablen und 100
Nebenbedingungen berechnet der Algorithmus also Schnittpunkte, und in der Realität treten noch viel größere Zahlen auf. Man muß nur bedenken, wieviele verschiedenartige Produkte ein Supermarkt im Sortiment hat. Wenn man einen Computer hätte, der 100 Mrd.
Schnittpunkte pro Sekunde bearbeiten könnte, so würde
dieser ca. Somit benötigt man einen wesentlich schnelleren und wirtschaftlicheren Algorithmus, um lineare Optimierungsaufgaben zu lösen. |
||
3.6 Der Simplexalgorithmus |
||
3.6.1 Die Idee des Simplexalgorithmus |
||
| Für die Lösung linearer Optimierungsaufgaben
betrachtet man lokal eine Ecke des Polyeders. Von dieser
Ecke ausgehend wählt man eine der benachbarten Ecken, so
daß man dem Optimum näher kommt. Man betrachtet von
dieser neuen Ecke ausgehend wieder die benachberten
Ecken, und fährt so fort, bis eine optimale Ecke erricht
ist. Wenn man dabei aber naiv vorgeht, jeweils alle benachbarten Ecken betrachtet, an allen Ecken den Wert der Zielfunktion berechnet und so die jeweils nächste Ecke bestimmt, dann hat man nichts gewonnen und benötigt wieder viel zu viele Iterationsschritte. Damit der Algorithmus schnell genug ist, muß man die jeweils nächste Ecke allein aus der mathematischen Darstellung der jeweils aktuellen Ecke und der Zielfunktion gewinnen. Dafür benötigt man eine geschickte Darstellung der Optimierungsaufgabe, die eine geschickte Wahl der nächsten Ecke erlaubt. |
||
3.6.2 Zur Geschichte des Simplexalgorithmus |
||
| Mit ersten Untersuchungen zu diesem Thema begründete
der sowjetische Mathematiker Kantorowitsch 1939 die
'Lineare Optimierung'. Eine geschickte Darstellung von
Optimierungsaufgaben zusammen mit einer Vorschrift für
die geschickte Wahl der jeweils nächsten Ecke wurde
bereits im Jahr 1942 von G.B.Dantzig [6] veröffentlicht,
der zugehörige Algorithmus wird Simplexalgorithmus
genannt. Empirisch wurde rasch festgestellt, daß der Simplexalgorithmus höchstens max(n, m) Iterationsschritte benötigt, wenn n die Anzahl der Variablen und m die Anzahl der Nebenbedingungen ist. Da er also schnell und gut verwendbar ist, wurde er sehr bald allgemein bekannt. Seine Bedeutung ist mit der rasanten Entwicklung der Computer seit den 60er Jahren noch gewachsen, denn dadurch war es möglich, immer größere Datenbestände in immer kürzerer Zeit zu verarbeiten. Bereits mit den noch nicht sehr leistungsstarken Computern in den 60er Jahren wurden schon erstaunliche Ergebnise mit dem Simplexalgorithmus erreicht. So wird z.B. berichtet, daß man 1963 eine Computeraufgabe mit ca. zwei Millionen Variablen gelöst hat [7]. |
||
3.6.3 Beschreibung des Simplexalgorithmus |
||
| Ausgangspunkt für den Simplexalgorithmus ist die
Darstellung der linearen Optimierungsaufgabe mit den
Schlupfvariablen (vgl. Abschnitt 2.2.1): mit |
||
Man kann für jeden Punkt  im n-dimensionalen,
reellen Raum das (n+m)-Tupel 
so berechnen, daß die Nebenbedingungsgleichungen
erfüllt sind. Punkte auf dem Rand des Planungsgebiets
zeichnen sich dadurch aus, daß die zugehörige
Komponente in diesem (n+m)-Tupel =0 ist.
Schnittpunkte von jeweils n Hyperebenen kann man
also daran erkennen, daß mindestens n
Komponenten = 0 sind. |
||
| Das Simplextableau | ||
| Zur Vereinfachung kann man die Optimierungsaufgabe
durch das sogenannte Simplextableau
beschreiben. Dabei beginnt der Simplexalgorithmus mit dem
sogenannten Starttableau. |
||
In der ersten Zeile stehen die Variablennamen,
darunter die zugehörigen Koeffizienten der
Nebenbedingungen und in der letzten Zeile, Zielzeile genannt, ist
die Zielfunktion dargestellt. Dabei steht unten rechts
z.B. Z, Z-2, Z-1000, je nach dem Wert von  . Z
steht als Zeichen für die Zielfunktion und wird im
folgenden wie eine formale Variable behandelt. |
||
Man erkennt eine Ecke des Planungsgebiets daran, daß
m Spalten eine Einheitsmatrix bilden. Der Wert
der zugehörigen Variablen findet man in der  -Spalte
auf der gleichen Höhe wie die jeweilige 1, die
restlichen Variablen haben den Wert 0. Das Starttableau
entspricht also der Ecke  bzw. dem Tupel  ,
der sogenannten Nulllösung. |
||
| Nun stellt sich die Frage, wie man durch Umformung
des Simplextableaus von einer Ecke zur nächsten gelangt,
und zwar derart, daß sich dabei nach wenigen Schritten
der maximale Wert der Zielfunktion einstellt, und wie man
feststellt, daß ein Maximum erreicht ist und wie dieses
aus dem Tableau abgelesen werden kann. Den Übergang von einem Tableau zum nächsten nennt man Pivotschritt. Er geschieht durch Veränderung der Einheitsmatrix. In einer der Spalten, die nicht zur Einheitsmatrix gehören, wird durch elementare Zeilenumformungen ein Element zu 1 und die anderen zu 0. Dadurch wird diese Spalte Teil der Einheitsmatrix. Eine andere Spalte wird durch die elemetaren Zeilenumformungen aus der EInheitsmatrix entfernt und die dazugehörige Variable hat in der neuen Ecke den Wert 0. Dasjenige Element im Tableau, das zur 1 werden soll, heißt Pivotelement. Da das Pivotelement die nächste Ecke festlegt, steckt in den Kriterien zur Auswahl der Kern des Simplexalgorithmus. Aus diesem Grund wurde in der Unterrichtsreihe auf diesen Aspekt besonderen Wert gelegt. |
||
| Die Wahl des Pivotelements und das Abbruchkriterium | ||
| Das Pivotelement
ist der Schnittpunkt einer Pivotspalte und einer
Pivotzeile. Dabei wählt man die Pivotspalte so,
daß der Wert der Zielfunktion am schnellsten wächst.
Damit man den zulässigen Bereich nicht verläßt,
springt man zur benachbarten Ecke und wählt die
Pivotspalte entsprechend. 1. Auswahl der Pivotspalte: Unter den positiven Elementen der Zielzeile wählt man das größte. Die darüberliegende Spalte ist die Pivotspalte. 2. Auswahl der Pivotzeile:
Unter allen positiven Elementen 3. Abbruchkriterium: Wenn in der letzten Zeile keine positiven Zahlen mehr stehen, ist das Maximum erricht. Bemerkung: Wenn es in der Pivotspalte keine positiven Zahlen gibt, dann gibt es kein Maximum. |
||
| Der Pivotschritt unter Verwendung des Gaußverfahrens | ||
| Die elementaren Zeilenumformungen beim Pivotschritt
entsprechen denen beim Gaußverfahren zur Lösung von
linearen Gleichungssystemen. Bei der Anwendung ist dabei
darauf zu achten, daß die Pivotzeile durch das
Pivotelement dividiert wird, und dann die
Zeilenumformungen an den restlichen Zeilen
einschließlich der Zielzeile vorgenommen werden. Dabei
darf nur ein Vielfaches der Pivotzeile von den anderen
Zeilen subtrahiert werden. Als Ergebnis erhält man nach dem Pivotschritt ein neues Tableau, das eine neue Ecke charakterisiert und mit dem man sich dem Maximum genähert hat. Wenn das Maximum noch nicht erreicht ist, dann wählt man nun wieder ein Pivotelement, rechnet das Tableau mit dem Gaußverfahren um und fährt so fort. Mit endlich vielen Tableaus erricht man so stets das Maximum. |
||
| zurück zum Inhalsverzeichnis | ||
3.7 Modellbildung und Interpretation |
||
| Ausgangspunkt bei der linearen Optimierung ist stets ein problem der realen Welt, für das man ein bestmögliches Ergebnis sucht. In meiner Unterrichtsreihe wurde stets nach einem Gewinn ader ertrag gefragt. | ||
Um ein Optmum zu finden, geht man in drei Schritten
vor.
|
||
| Bei der Modellbildung werden aus dem gegebenen realen Problem Variablen und die Zielfunktion ermittelt. Nun sind die real existierenden ressourcen jedoch in der Regel begrenzt, und diese Begrenztheit muß sich im Modell wiederfinden. Dafür wird der Definitionsbereich der Funktion auf den Teilbereich der jeweils zur Verfügung stehenden Ressourcen littels Nebenbedingungen eingeshränkt. | ||
| Bei der Interpretation des Ergebnisses in Bezug auf das ursprüngliche Problem aus der realen Welt genügt der optimale Wert der Zielfunktion in der Regel nicht. Vielmehr ist zusätzlich von Interese, wieweit jede einzelne Nebenbedingung ausgelastet wird, d.h. wieviel bei der optimalen Lösung von jeder einzelnen Ressource verbraucht wird. Da der Rest in der realen Welt weiterverwendet werden kann, nennt man ihn freie Kapazität. | ||
| Im Simplextableau kann man die Werte für die
Interpretation leicht ablesen. Der jeweilige
Zielfunktionswert steht unten rechts. Beispielsweise
bedeuten Z - 10 ein Maximum in Höhe von 10.
Die Werte der Variablen kann man an der -Spalte
ablesen (vgl. Abschnitt 3.6.3). Die freien Kapazitäten
sind die Werte der Schlupfvariablen, die Differenzen zu
den Ressourcen die Auslastungen. Auch die Pivotwahl
läßt sich leicht kontrollieren: Wenn in der -Spalte
negative Zahlen stehen, dann war die Pivotwahl falsch. Modellbildung und Interpretation gehören zur Betrachtung der linearen Optimierung und waren deshalb Bestandteil meiner Unterrichtsreihe. |
||
3.8 Ein Beispiel |
||
| zurück zum Inhaltsverzeichnis | ||
4. Einige Bemerkungen zur Planung meiner Reihe |
||
4.1 Lernziele der Reihe |
||
Die Lernziele der Reihe waren folgende:
|
||
4.2 Aufbau der Reihe |
||
| Im Mittelpunkt der Reihe stand die Begegnung der Schülerinnen und Schüler mit einem algorithmischen Prozeß, dem Simplexalgorithmus. Es kam in besonderer Weise darauf an, denselben Prozeß mit verschiedenen Methoden (Zeichnung, Rechnung) und mit verschiedenen Medien (Papier, Computer) in Gang zu setzen. | ||
Die Reihe war in zwei Blöcke unterteilt:
|
||
| Der erste Block umfaßte bei mir drei
Unterrichtsstunden, der zweite neun. Eine besondere
Vertiefung des Simplexverfahrens sollte durch von den
Schülern selbst zu erstellende Aufgaben am Ende der
Reihe erfolgen. Dafür reichte die Zeit jedoch nicht. Sie
wurden an die Reihe angehängt. Die beiden Lösungsverfahren wurden nicht unabhängig voneinander betrachtet. Der Simplexalgorithmus sollte nicht als eine vom bisherigen losgelöste weitere Lösungsmethode, die scheinbar zufällig auf die gleiche Lösung führt, vorgestellt werden. Stattdessen sollten die Schüler die wesentlichen Aspekte des Simplexverfahrens am Graphen wiedererkennen, wie z.B. die Wahl der Pivotspalte und -zeile, und damit das "Eckenwandern" durch die Tableauumformungen direkt graphisch nachvollziehen. Außerdem ermöglicht eine solche Vorgehensweise den Schülern, ihren Blick für die wechselseitige Abhängigkeit von geometrischen und algorithmischen Zusammenhängen zu schärfen. Somit erfolgte die Erarbeitung des Simplexalgorithmus an einem bereits graphisch gelösten Optimierungsproblem. Die parallele Veranschaulichung am Graphen trug deutlich zum Verständnis des algorithmischen Prozesses bei. Auch bei der Erarbeitung der notwendigen Begrifflichkeiten und Abläufe war die parallele Veranschaulichung an der Graphik für die Schüler sehr hilfreich, z.B. für das Auffinden von Pivotspalte und -zeile. Bem.: Für diese "parallele" Betrachutng bietet sich nicht jede beliebige Aufgabe an, da das zweidimensionale Problem durch die Einführung der Schlupfvariablen noch höher dimensional wird. So kann es sein, daß die "Eckenwanderung" über eine nicht dargestellte bzw. nicht darstellbare Dimension stattfindet. |
||
| Der Simplexalgorithmus zeigte sich sowohl für gute als auch für schwächere Schüler geeignet. Für die guten Schüler war die Erarbeitung des Algorithmus eine kognitive Herausforderung. Bei der Anwendung des Simplexverfahrens konnten auch die schwächeren Schüler selbstständig aktiv werden und das Verfahren nachahmen. | ||
4.3 Zur Auswahl der Aufgaben |
||
| In meiner Reihe habe ich schwerpunktmäßig
Textaufgaben eingesetzt, da die Schüler die lineare
Optimierung zur Lösung ökonomischer Fragestellungen
kennenlernen sollten. In der Reihe wurden die linearen Optimierungsprobleme auf Maximierungsprobleme beschränkt. Dies hatte folgenden Grund: Um den Simplexalgorithmus anzuwenden, wird eine Startlösung gebraucht. Als besonders einfache Startlösung bietet sich die sogenannte Nulllösung an (vgl. Abschnitt 3.6.3). Diese ist für das reguläre Simplexverfahren (vgl. Abschnitt 3.1) immer möglich. Um Probleme zu lösen, die die Null nicht als Startlösung (Ecke) haben, bräuchte man aufwendigere Verfahren, z.B. Simplex Phase I (vgl. [5], S.214ff), die dem regulären Simplex voranzustellen wären. Diese kennenzulernen, würden aber den Rahmen der Reihe sprengen. Mit dem graphischen Verfahren kann man natürlich auch Minimierungsprobleme lösen. Um einen einheitlichen Bogen vom graphischen Verfahren zum Simplexalgorithmus zu schlagen, habe ich allerdings darauf verzichtet. |
||
| Innerhalb der Vertiefungsaufgaben zum
Simplexalgorithmus habe ich die Anwendung i.w. auf einen
Aufgabentyp beschränkt, um dem Problem der Modellbildung
nicht zuviel Raum einzuräumen, so daß das Einüben des
Simplexverfahrens darunter leiden könnte. Wenn man nicht
mehr durch eine Examensreihe eingeschränkt ist, läßt
sich das variabler gestalten. Der verwendete Aufgabentyp, von mir als Mischungsaufgabe bezeichnet, ist dadurch gekennzeichnet, daß man Rohstoffe in vorgegebenen Verhältnissen zu Endprodukten mischt und dann nach der ertragreichsten Mischung fragt. Für diesen Aufgabentyp gibt es viele Beispiele aus der Realität. Für die Schüler ist dieser Aufgabentyp recht anspruchsvoll, denn es ist nicht immer einfach für sie, der Textaufgabe die richtigen Mischungsverhältnisse zu entnehmen. Andererseits zwingt dieser Aufgabentyp die Schüler, sich mit der Modellbildung und Interpretation der Aufgabe besser auseinanderzusetzen und mathematische Modelle an der Wirklichkeit zu überprüfen. |
||
4.4 Zum Computereinsatz |
||
| Der Computer ist ein nicht mehr wegzudenkendes
Hilfsmittel im Alltag geworden. So sollten ihn die
Schüler als hilfreiches Werkzeug im Mathematikunterricht
kennenlernen. Der Simplexalgorithmus legt wie jeder
Algorithmus den Einsatz dieses Mediums besonders nahe. Beim Einsatz des Computers ist zu entscheiden, welche und wieviel Arbeit er den Schülern abnehmen soll. Er könnte alle Schritte (Pivotelementsuche und Pivotierung) übernehmen, so daß die Schüler nur die mathematischen Formeln eingeben müßten und der Rechner das Endergebnis ausgibt. Dies käme einer "Mathematik auf Knopfdruck" nah und sollte hier nicht verfolgt werden. In der Unterrichtsreihe sollte der Computer für große Systeme den Rechenaufwand der Pivotierung erleichtern. So blieb mehr Raum für die entscheidenden Schritte der Pivotelementauswahl, die von den Schülern wie bei den Aufgaben ohne Computerhilfe durchzuführen waren. |
||
| Als Software wurde das Computeralgebrasystem Derive eingesetzt. Es gibt ein Programm von Josef Böhm [2]. Dieses Programm weicht aber in der Notation von der für diese Unterrichtsreihe gewählte Form der Tableaus und Pivotierung stark ab. So habe ich selbst ein Programm für DERIVE geschrieben, das den Schülern ermöglichte, die Tableaus aufzubauen und zu bearbeiten, wie sie es von den vorherigen Aufgaben kannten. Das Programm und seine Dokumentation können heruntergeladen werden. | ||
| Der Medienwechsel zum Computer wurde von den Schülern sehr positiv aufgenommen. Durch seinen Einsatz konnten sie sich einem umfangreicheren Problem widmen. Außerdem wirkte er Ermüdungserscheinungen vor. Jeder, der sich mit Gaußumformungen beschäftigt hat, kennt die Erfahrung, wie mühselig das Rechnen mit Papier und Bleistift sein kann und wie schnell man sich dabei verrechnet und somit falsche Ergebnisse erhält. Diese Umformungen hat ihnen der Computer abgenommen, so daß sie sich auf die entscheidenden neuen Aspekte dieses Algorithmus und die Interpretation seiner Ergebnisse konzentrieren konnten. | ||
| Wie immer beim Einsatz von Computern muß eine Einarbeitungsphase eingeplant werden, die es den Schülern ermöglicht mit der Bedienung des Rechners und dem Programm vertraut zu werden. Dafür bietet sich z.B. an, einige bereits gelöste Aufgaben am Computer durchzurechnen. Die Schüler können dann die Reaktion des Rechners auf ihre Eingaben anhand ihrer Aufzeichnungen überprüfen und eine eventuell falsche Bedienung erkennen. | ||
4.5 Aufgaben selbst ausdenken |
||
| Eine Vertiefung besonderer Art stellt das
Selbstausdenken von Aufgaben dar. Bei der Entwicklung
eigener Aufgaben können die Schüler zum einen kreativ
werden, zum anderen gewinnen sie dadurch einen tieferen
Einblick in die Struktur der Aufgaben. Bei den linearen Optimierungsaufgaben müssen die Schüler z.B. selbst erkennen, welche Nebenbedingungen notwendig sind, damit das Problem lösbar ist. Zusätzlich kommen hier Aspekte wie Originalität, Veränderungsgrad gegenüber bisherigen Aufgaben und Präzision der Formulierung hinzu. So sollte sich zum Abschluß der Reihe jeder Schüler als Hausaufgabe eine lineare Optimierungsaufgabe ausdenken. |
||
| Die Resultate der Schüler deuteten mit ihrem Ideenreichtum auf Spaß an dieser Art von Aufgabe hin. Die meisten Aufgaben haben die äußere Form der linearen Optimierung gut getroffen: die Aufgaben beinhalteten die Variablen, die Nebenbedingungen und die Zielfunktion. Allerdings fehlten des öfteren Nebenbedingungen, so daß die Aufgabe in der gestellten Form nicht gelöst werden konnte, sondern z.B. erst Ergänzungen erfolgen mußten. Hier zeigt es sich, daß eine Beschäftigung mit dieser Art Hausaufgabe noch viele Möglichkeiten bietet, das Verständnis der Schüler gegenüber dem Thema zu vertiefen. | ||
| In Anhang 6.3 habe ich den Wortlaut einiger Schüleraufgaben wiedergegeben. | ||
| zurück zum Inhaltsverzeichnis | ||
5. Literatur |
||
| [1] Schöwe, R., Knapp, J. und Borgmann, R.: Mathematik
zur Fachhochschulreife, Analysis und lineare Algebra;
Cornelsen Verlag, Berlin, 1. Auflage, 1996 [2] Böhm, Josef: Von der graphischen Lösung linearer Ungleichungssysteme zur Simplexmethode mit DERIVE und dem TI-92; aus "Computeralgebra im Mathematikunterricht", ZKL-Texte Nr.6, Münster, 1998 [3] Stoer, Joseph: Einführung in die Numerische Mathematik I; Springer-Verlag, Berlin Heidelberg NewYork Tokyo, vierte Auflage, 1983 [4] Bronstein, I.N. und Semendjajew, K.A.: Taschenbuch der Mathematik; Verlag HARRI DEUTSCH, Thun und Frankfurt/Main, 23. Auflage, 1987 [5] Press,William H. und andere: Numerical Recipes in C, The Art of Scientific Computing; Cambridge University, second edition, 1992 [6] Dantzig, G.B.: Linear Programming and Extensions; NJ: Princeton University Press, Princeton, 1963 [7] Die Software Schmiede: WinFunktion, Mathematik von A bis Z ; bhv Verlag Bürohandels- und Verlagsgesellschaft mbH, Korschenbroich, 1995 [8] Kultusministerium Nordrhein-Westfalen: Richtlinien für die gymnasiale Oberstufe; Verlagsgesellschaft Ritterbach mbH, Frechen, unveränderter Nachdruck, 1991 [9] Ministerium für Schule und Weiterbildung, Wissenschaft und Forschung des Landes Nordrhein-Westfalen: Richtlinien und Lehrpläne für die Sekundarstufe II; Ritterbachverlag GmbH, Frechen, 1. Auflage, 1999 [10] Tietze, Uwe-Peter und andere: Mathematik in der Sekundarstufe II; Band 1; Vieweg, Braunschweig/Wiesbaden, 1997 [11] Wittmann, Erich Ch.: Grundfragen des Mathematikunterrichts; Vieweg, Braunschweig, 1981 |
||
| zurück zum Inhaltsverzeichnis | ||
6. Anhang |
||
6.1 Das Computerprogramm (zum Downloaden) |
||
| Das Computerprogramm und seine
Dokumentation zum Herunterladen: download simplex.mth und download doku_sim.doc Bem.: Die Schüler haben ein abgespecktes Programm von mir bekommen. Außerdem kannten sie nur den Befehl zur Pivottierung (Pivotschritt(pr, pc)). Die anderen Möglichkeiten des Programms habe ich zur Erleichterung der Lösungen der Simplexaufgaben hinzugefügt. |
||
| Ein Beispiel | ||
6.2 Zwei selbsterdachte Aufgaben |
||
GruppenarbeitDas Problem ist der Werbebranche entnommen, da dieser Alltagsbereich die Schüler in der Regel gut emotional anspricht. Die Story und die Werte sind frei erfunden. Die Arbeitszettel (für vier Gruppen) unterscheiden sich allein im Werbebestand der Sender, um die Gruppenergebnisse später im Plenum unter der Fragestellung vergleichen zu können, welchen Vorschlag sie dem Vorstand ihres Senders geben müßten, damit dieser seinen Gewinn verbessert. Diese Diskussion soll den Schülern einen Eindruck davon geben, daß die Ermittlung einer sogenannten optimalen Lösung im Alltag allein nicht ausreicht, sondern daß man aus diesem Ergebnis Konsequenzen für eventuelle Verbesserungsmöglichkeiten ziehen muß. |
||
KlausuraufgabeHier geht es um Schokolade. Die Alternativaufgabe war für Schüler geplant, die mit der Modellbildung Probleme haben könnten. Sie sollten dennoch die Möglichkeit haben zu zeigen, daß sie das graphische Lösungsverfahren sowie den Simplexalgorithmus anwenden können. |
||
6.2 Aufgaben der Schüler |
||
| Bem.: Beispiel zwei und drei sind so noch nicht lösbar! | ||
Beispiel 1 |
||
| zurück zum Inhaltsverzeichnis | ||
| Startseite |
und 
mit i, j = 1, ...
, n.
mit i
= 1, ..., n bestimmen.
Jahre benötigen. Zum Vergleich: Die Erde
existiert vermutlich seit ungefähr 
Jahren.
minimal ist. Die zugehörige Zeile ist die
Pivotzeile.